Dada una función de transferencia que actúa como un filtro paso bajo:
| kill ( all ) $ dB ( x ) : = float ( 20 · log ( abs ( x ) ) / log ( 10 ) ) $ H : ωc / ( ωc + s ) ; |
Para una mejor compresión del comportamiento del filtro y facilidad en la visualización gráfica, asignamos la frecuencia de corte ωc=1
| (%i4) | ωc : 1 $ H : ev ( H ) |
con la ayuda de la utilidad coma ,
(pueden saber más acerca de coma aquí: https://www.austromath.at/daten/maxima/zusatz/Control_Engineering_with_Maxima.pdf)
como nos ayuda visualiza rápidamente donde estarían situados en el plano los ceros y polos de la función de transferencia, así comportamiento del filtro en el plano complejo.
| (%i10) | load ( «coma» ) $ poles_and_zeros ( H ) ; magnitude_plot ( H ) ; |
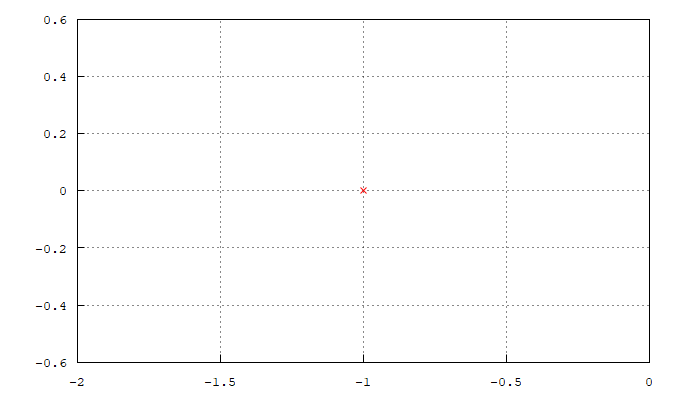
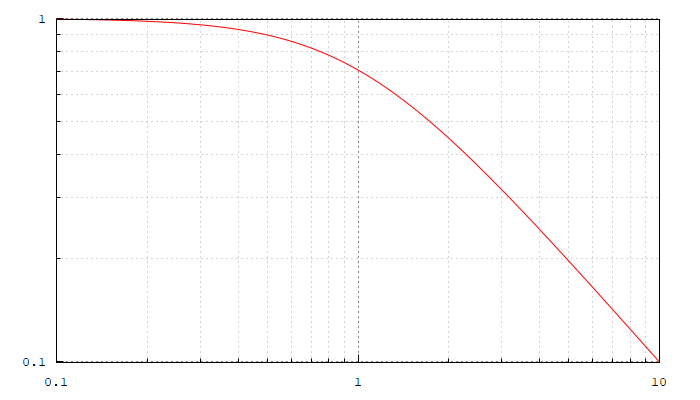
Lo que nos dice coma es que el polo de la función de transferencia está situado en el plano complejo, y que además en la frecuencia de corte (1) tenemos una atenuación de la señal 70%.
como el plano complejos está formado por los siguientes componentes: s:x+%i*y;
| –> | s : x + %i · y $ |
definimos la función de transferencia en dB, y podemos representar en 3D el plano s y la representación del comportamiento del filtro:
| (%i14) | define ( h ( x , y ) , dB ( cabs ( H ) ) ) $ /*salida en DB*/ wxplot3d ( h ( x , y ) , [ x , − 4 , 2 ] , [ y , − 3 , 3 ] , [ z , − 10 , 25 ] , [ xlabel , «x» ] , [ ylabel , «%i» ] , [ legend , «Función de transferencia 3D» ] ) ; |
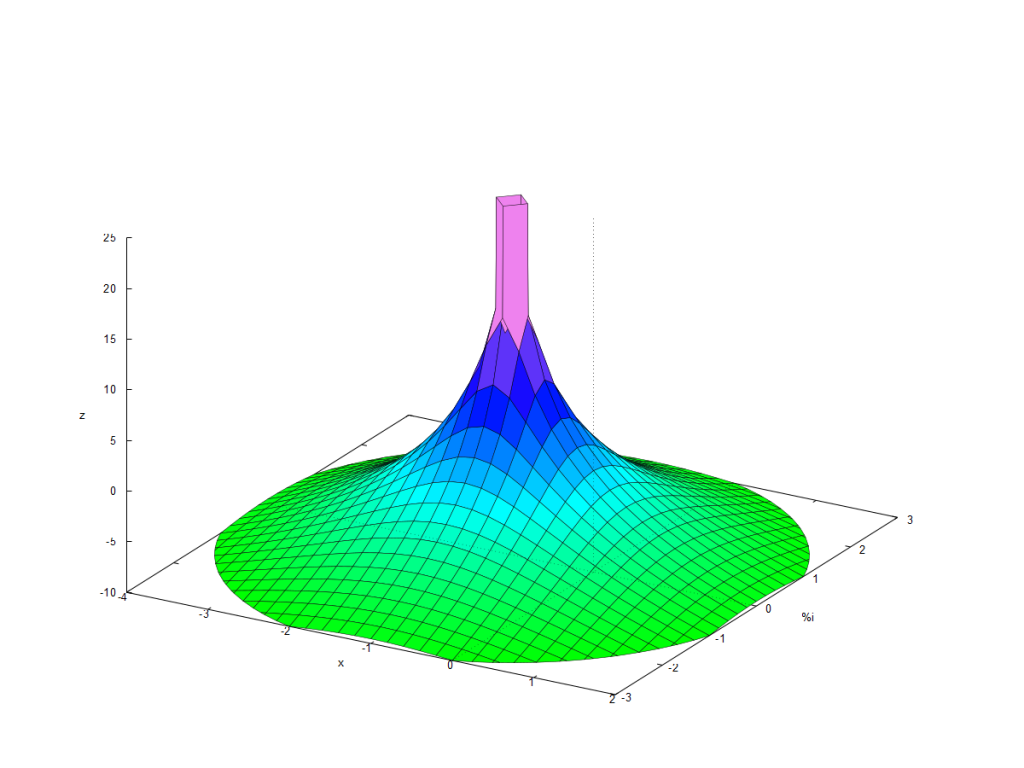
ahora para la función propuesta con un polo y un cero
| (%i2) | kill ( all ) $ dB ( x ) : = float ( 20 · log ( abs ( x ) ) / log ( 10 ) ) $ H : s / ( ωc + s ) ; |
asignamos el punto de corte de la frecuencia a la unidad para una más fácil compresión del comportamiento del filtro en coma
| (%i4) | ωc : 1 $ H : ev ( H ) ; |
vemos que es lo que nos muestra coma
| (%i15) | load ( «coma» ) $ poles_and_zeros ( H ) ; magnitude_plot ( H ) ; |
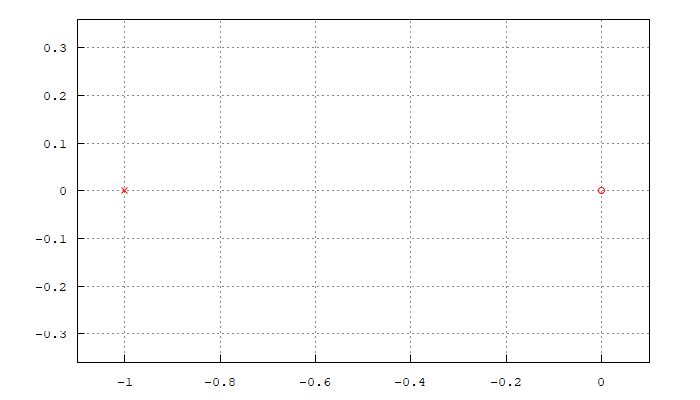
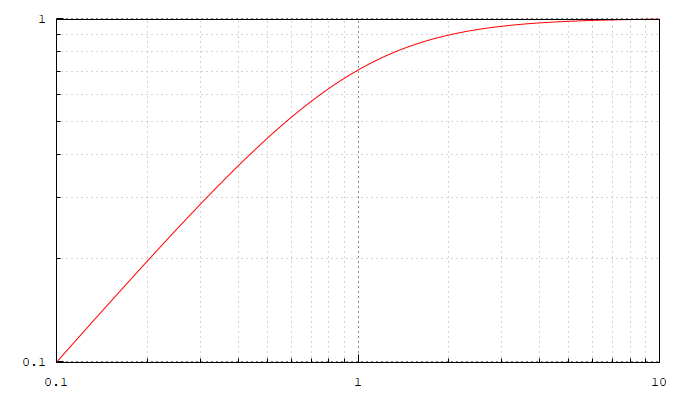
vemos que el polo se sitúa en el eje x en -1 y cero se sitúa justo en el 0,
y vemos que tenemos el comportamiento de un filtro pasa alta, con el punto de corte en 1 la frecuencia de corte asignada con una atenuación en ese punto del 70%.
Para grafiar el plano complejo en 3D procedemos como anteriormente.
| (%i20) | s : x + %i · y $ define ( h ( x , y ) , dB ( cabs ( H ) ) ) $ /*salida en DB*/ wxplot3d ( h ( x , y ) , [ x , − 4 , 2 ] , [ y , − 3 , 3 ] , [ z , − 10 , 25 ] , [ xlabel , «x» ] , [ ylabel , «%i» ] , [ legend , «Función de transferencia 3D» ] ) ; |
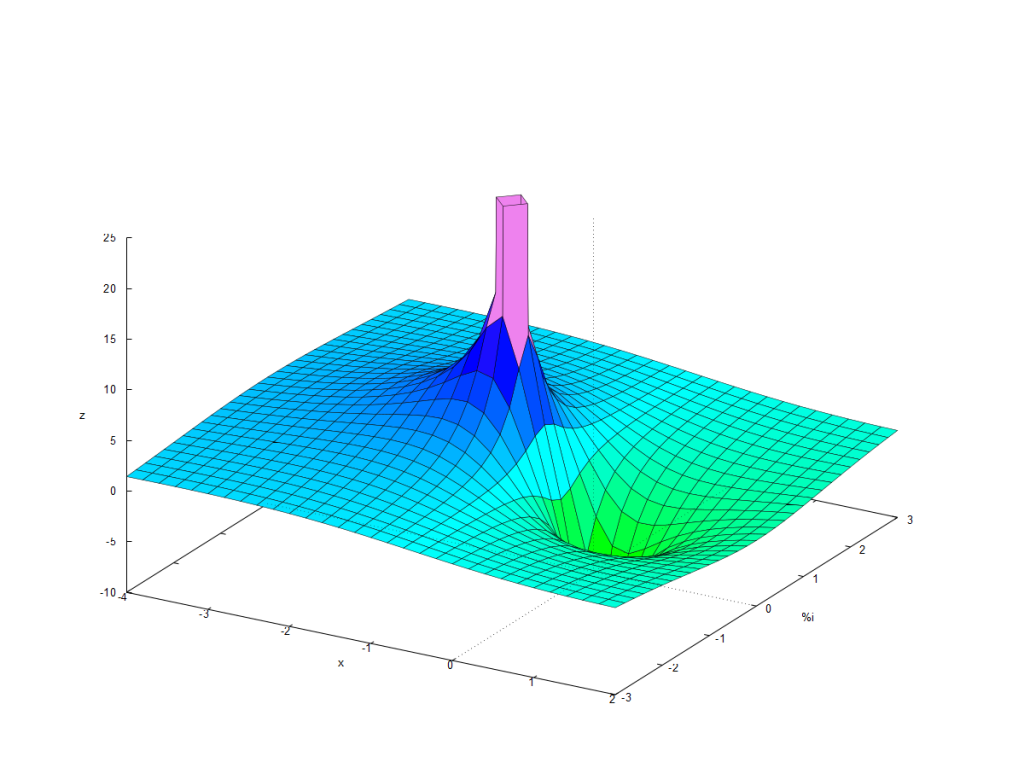
Para la siguiente función de transferencia con dos polos conjugados sería de la siguiente forma:
| (%i2) | kill ( all ) $ dB ( x ) : = float ( 20 · log ( abs ( x ) ) / log ( 10 ) ) $ H : ( ωc ) ^ 2 / ( s ^ 2 + 2 · δ · ωc · s + ( ωc ) ^ 2 ) ; |
donde δ es la resonancia o amortiguación en la frecuencia de corte y para facilitar la representación en coma asignamos los siguientes valores a la resonancia y a la frecuencia de corte:
| (%i6) | δ : 0 . 05 $ /*resonancia*/ ωc : 1 $ |
y nos queda la siguiente función de transferencia para representar con la ayuda de coma
| (%i7) | H : ev ( H ) ; |
y este es el resultado que nos muestra coma
| (%i13) | load ( «coma» ) $ poles_and_zeros ( H ) ; magnitude_plot ( H ) ; |
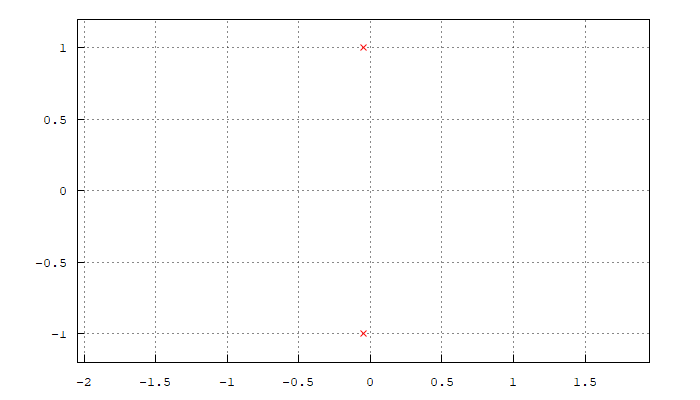
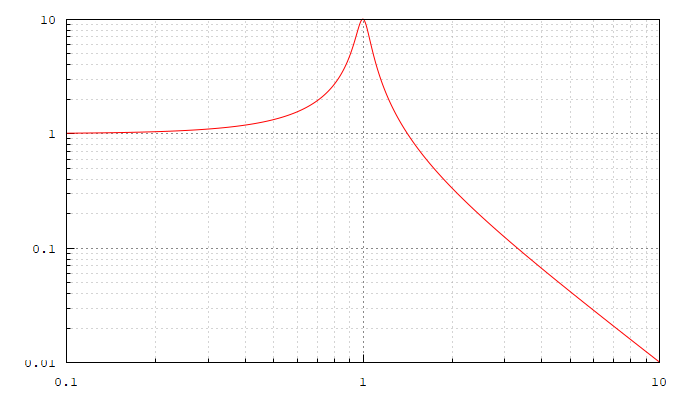
vemos como la función de transferencia filtra la señal en forma de filtro paso bajo con resonancia en la frecuencia de corte
La representación 3D del plano complejo del filtro con los polos conjugados
| (%i19) | s : x + %i · y $ define ( h ( x , y ) , dB ( cabs ( H ) ) ) $ /*salida en DB*/ wxplot3d ( h ( x , y ) , [ x , − 2 , 2 ] , [ y , − 3 , 3 ] , [ z , − 10 , 25 ] , [ xlabel , «x» ] , [ ylabel , «%i» ] , [ legend , «Función de transferencia 3D» ] ) ; |
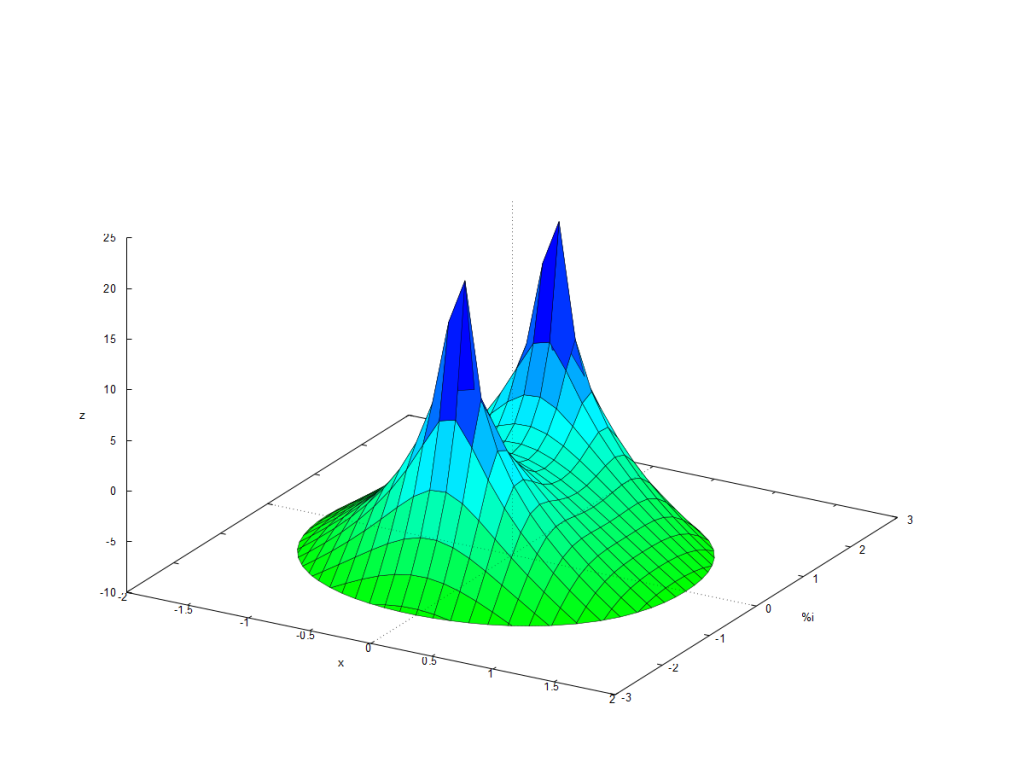
Vamos a aprovechar la función de animación que tiene Maxima para ir variando la resonancia de polos conjugados y ver como afecta al comportamiento del filtro.
| (%i4) | kill ( all ) $ dB ( x ) : = float ( 20 · log ( abs ( x ) ) / log ( 10 ) ) $ H : ( ωc ) ^ 2 / ( s ^ 2 + 2 · δ · ωc · s + ( ωc ) ^ 2 ) $ ωc : 1 $ fli : create_list ( ev ( H ) , δ , [ 0 . 05 , 0 . 1 , 0 . 3 , 0 . 5 , 0 . 8 , 0 . 9 , 1 . 0 , 0 . 9 , 0 . 8 , 0 . 5 , 0 . 3 , 0 . 1 , 0 . 05 ] ) $ /*resonancia*/ |
con la ayuda de coma vemos como a medida que aumentamos la resonancia, los polos conjugados se van juntado en el planos s y eso provoca el aumento magnitud de la señal en el punto de corte del filtro.
| (%i10) | load ( «coma» ) $ poles_and_zeros ( fli ) ; magnitude_plot ( fli ) ; |
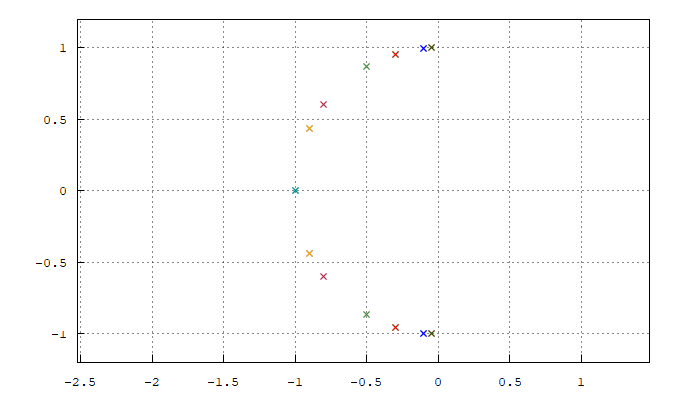
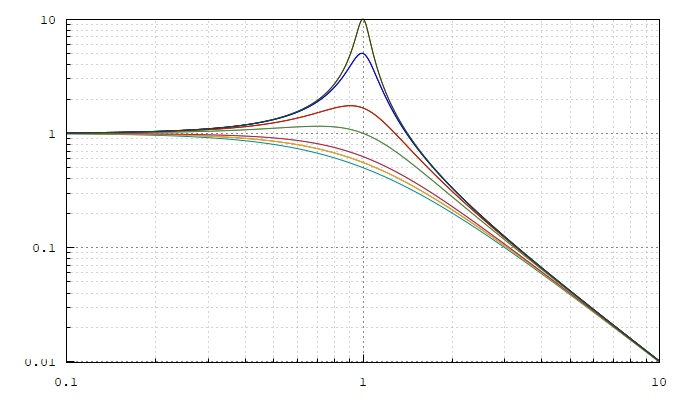
ahora vamos representar la animación de los polos en en el plano complejo al aumentar la resonancia
| (%i14) | s : x + %i · y $ fli : ev ( fli ) $ fz : dB ( float ( cabs ( fli ) ) ) $ with_slider_draw3d ( i , [ 1 , 2 , 3 , 4 , 5 , 6 , 7 , 8 , 9 , 10 , 11 , 12 , 13 ] , title = concat ( «k=» , i − 1 ) , enhanced3d = true , xlabel = «x» , ylabel = «%i» , zlabel = «dB» , explicit ( fz [ i ] , x , − 1 . 5 , 0 . 5 , y , − 1 . 5 , 1 . 5 ) ) ; |
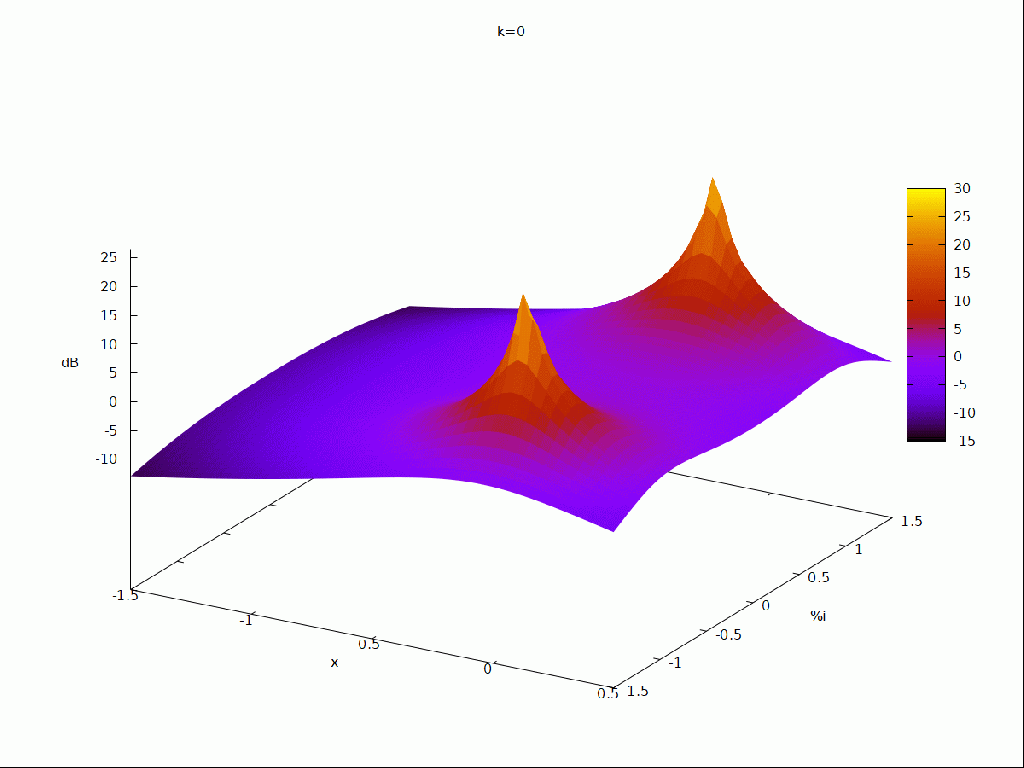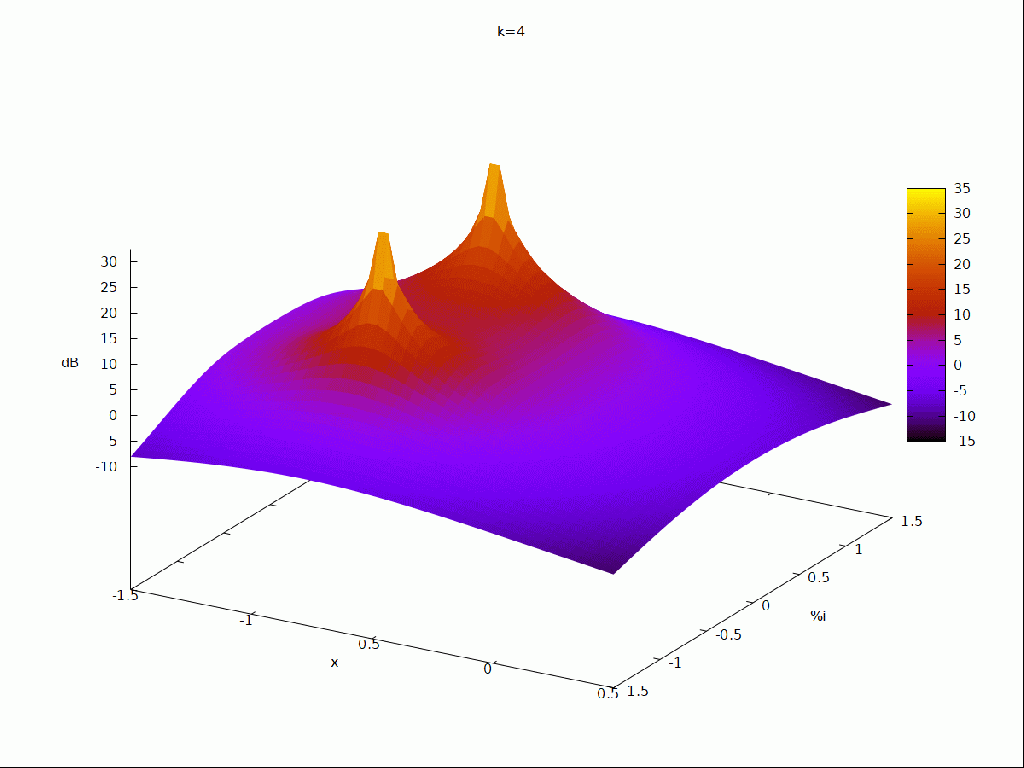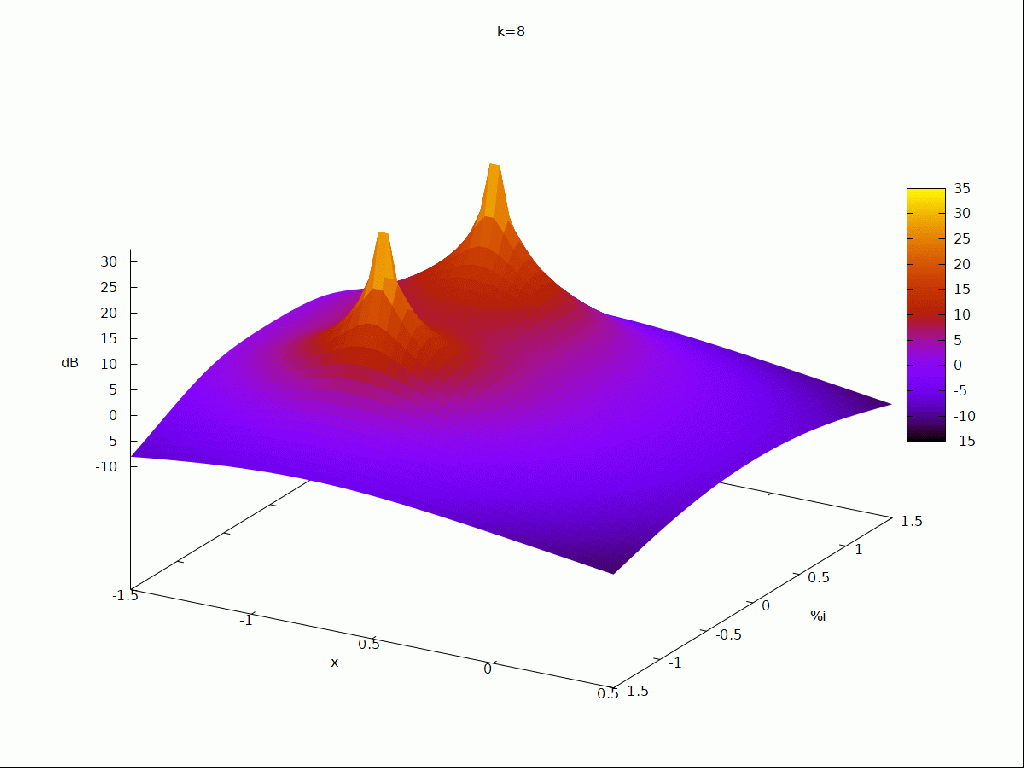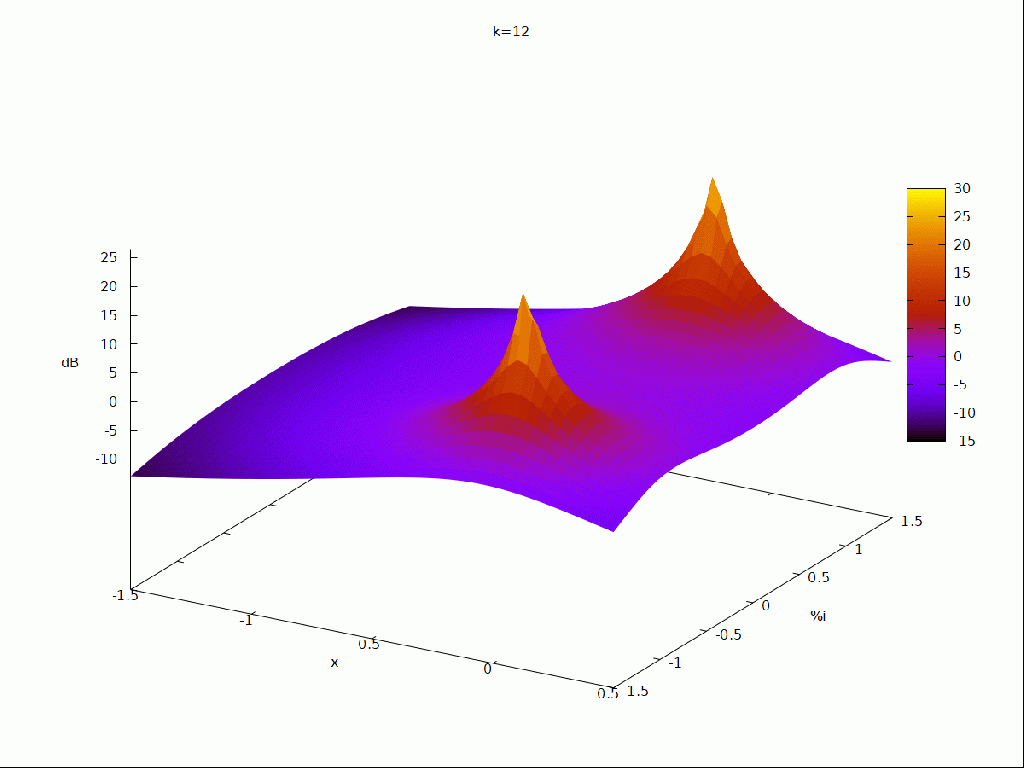
ya sólo nos queda realizar la animación del comportamiento de la función de tranferencia al aumentar la resonancia y como afectaría al procesado de la señal que pasará por este tipo de filtro.
| (%i7) | kill ( all ) $ dB ( x ) : = float ( 20 · log ( abs ( x ) ) / log ( 10 ) ) $ H : ( ωc ) ^ 2 / ( s ^ 2 + 2 · δ · ωc · s + ( ωc ) ^ 2 ) $ ωc : 1 $ s : %i · ω $ H : ev ( H ) $ fli : create_list ( ev ( H ) , δ , [ 0 . 05 , 0 . 1 , 0 . 3 , 0 . 5 , 0 . 8 , 0 . 9 , 1 . 0 , 0 . 9 , 0 . 8 , 0 . 5 , 0 . 3 , 0 . 1 , 0 . 05 ] ) $ /*resonancia*/ with_slider_draw2d ( i , [ 1 , 2 , 3 , 4 , 5 , 6 , 7 , 8 , 9 , 10 , 11 , 12 , 13 ] , xrange = [ 0 , 2 · %pi ] , yrange = [ − 25 , 25 ] , title = concat ( «k=» , i − 1 ) , xlabel = «ω(Frecuencia)» , ylabel = «dB» , logx = true , explicit ( dB ( cabs ( fli [ i ] ) ) , ω , 0 . 01 , 2 · %pi ) ) ; |
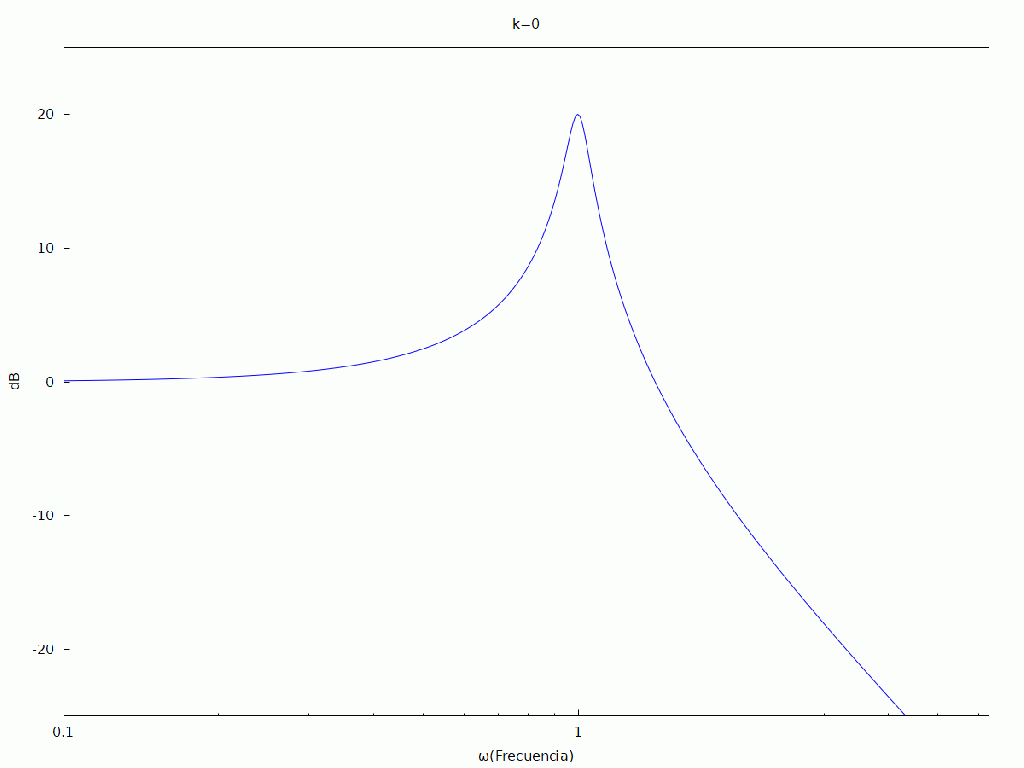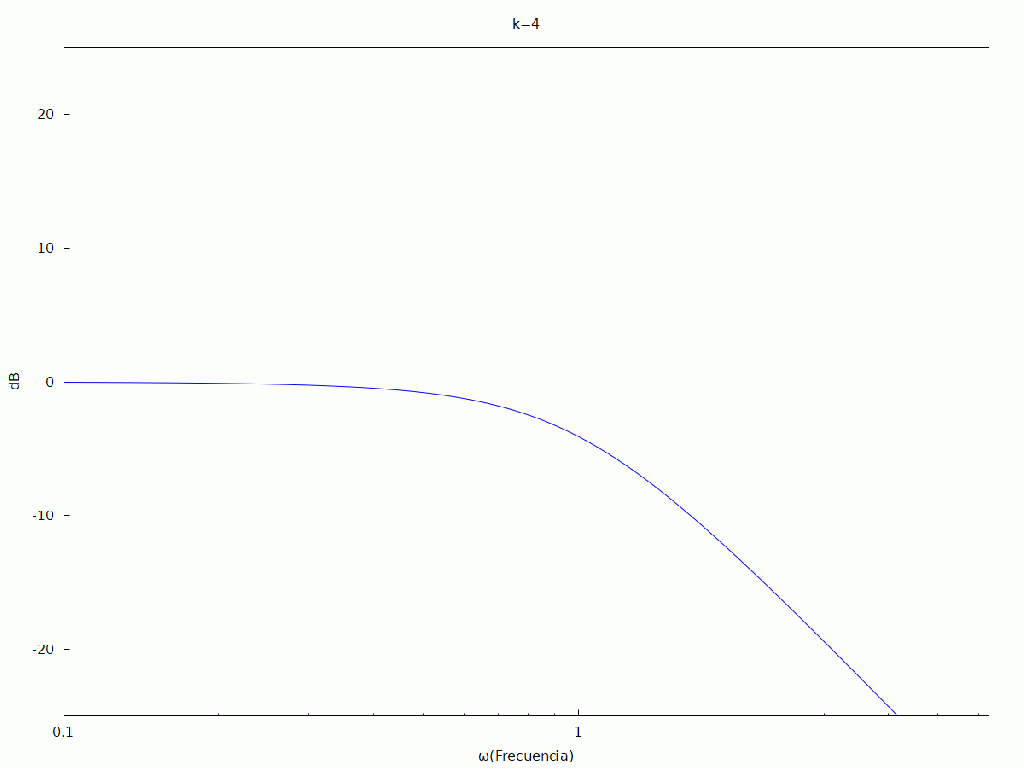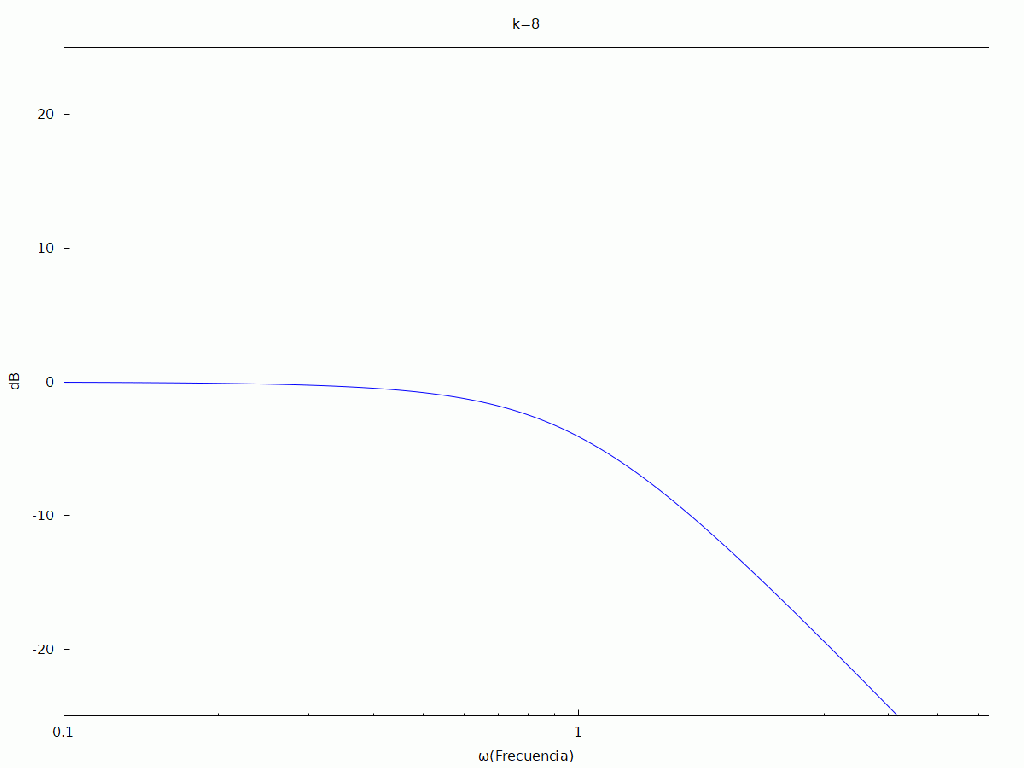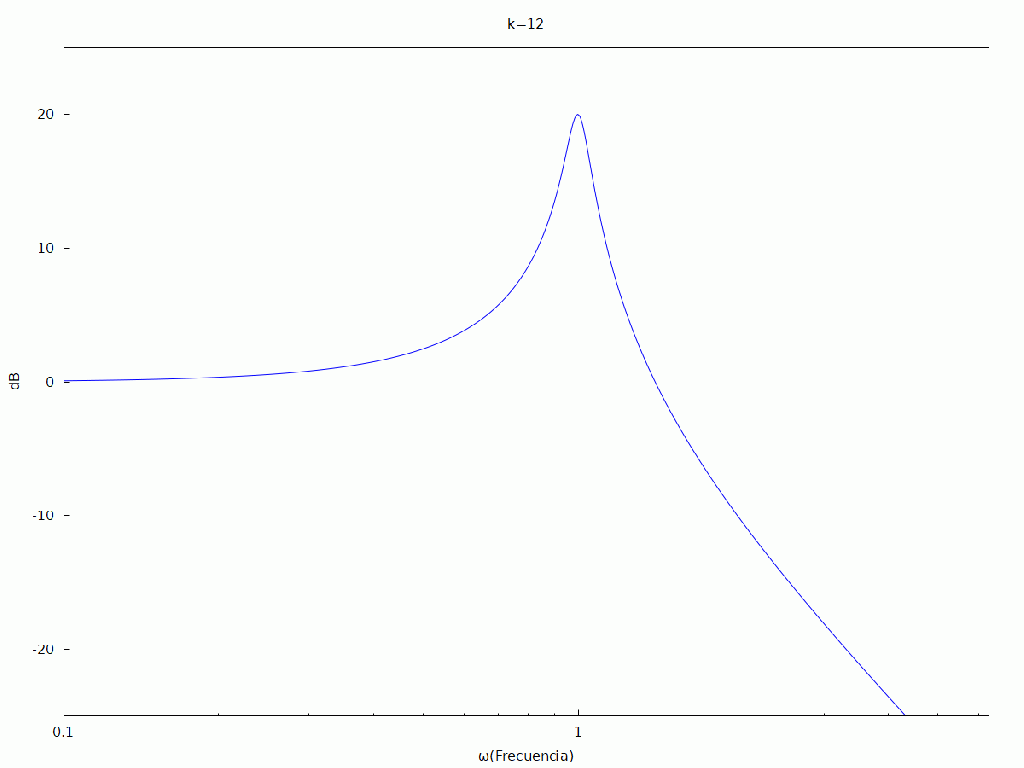
Deja un comentario